[科普中国]-博雷尔集

博雷尔代数

当X是一个度量空间时，博雷尔代数可以用如下生成的方法描述。2

对于X的一族子集T（即X的幂集P(X)的任何子集），令

Tσ为T中元素的可数并的全体

Tδ为T中元素的可数交的全体

Tδσ=(Tδ)σ.

现在利用超限归纳法定义如下的序列G，其中m是一个序数：

对于初始的情况，定义

G= X的所有开子集全体。

如果i不是极限序数，那么i是i-1的后继序数。令

G= [G]δσ

如果i是极限序数，令

我们现在可以说博雷尔代数是G，其中ω1是第一不可数序数，即势为ℵ₁的序数集。这意味着博雷尔代数可以通过开集全体的迭代运算

至第一不可数序而生成。

为了证明这一点，首先注意到度量空间中的任何开集都是一列递增紧集的并。特别地，易知对于任何极限序数m，集合的差运算将G映射到自身；而且，当m是不可数的极限序数时，G在可数并运算下是封闭的。

注意到对于每一个博雷尔集B，存在一个可数序数αB使得B可以通过αB多次迭代后得到。但是随着B取遍所有博雷尔集，αB也会相应地取遍所有可数序数，故而要得到所有博雷尔集所需的最靠前的序数是ω1，即第一不可数序数。

例子一个重要的例子，尤其是对于概率论而言，是实数集上的博雷尔代数。它是用来定义博雷尔测度的代数。对于概率空间上一个给定的实随机变量，其概率分布按照定义，也是一个博雷尔代数上的测度。

实直线R上的博雷尔代数是包含所有区间的最小σ-代数。

在利用超限归纳法构造时，可以证明在每一步中，集合的数量至多是连续统的幂。所有博雷尔集的总数不会多于。

非博雷尔集下面描述了卢津给出的一个实数集上的子集不是博雷尔集的例子。与之形成对比的是，不可测集的例子是无法给出的，不过其存在性是可以证明的。

每一个无理数都有一个唯一的连分数表示

其中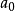是一个整数，其余的都是正整数。令A为对应序列的无理数组成的集合，而且其中的元素满足下列性质：存在一个无限子序列使得序列中每一个元素都是下一个元素的因子。这个集合A不是博雷尔集。事实上，这个集合是一个解析集，进一步地，在解析集全体构成的类中是完备的。