[科普中国]-仿射等价

概念

仿射等价(affine equivalence)是图形间的一种等价关系。若存在一个仿射变换把图形C1变成C2，则称C1与C2仿射等价。否则称为仿射不等价。图形的仿射等价是一种等价关系，即具有自反性、对称性、传递性。利用仿射等价关系可以把几何图形进行分类。同一类里的图形具有相同的仿射性质，不同类的两个图形间至少存在一个不同的仿射性质。仿射等价的概念在仿射几何中有广泛的应用。例如，利用圆和椭圆仿射等价的事实可以得到仿射变换的重要定理：平面上的仿射变换可以分解为一个正交变换和两个在互相垂直方向上的压缩(或伸长)的乘积。

仿射变换由有限次中心射影的积定义的两条直线间的一一对应变换称为一维射影变换。由有限次中心射影的积定义的两个平面之间的一一对应变换称为二维射影变换。1

因为正交变换、相似变换、仿射变换都保持共线三点的单比不变，必然保持共线四点的交比不变，所以这些变换都是射影变换。

如果平面上点场的点建立了一个一一对应，并且满足：

（1）任何共线三点的象仍是共线三点；

（2）共线四点的交比不变。

则这个一一对应叫做点场的射影变换，简称射影变换。

仿射几何几何学的一个分支学科。主要研究仿射空间中的图形在仿射对应(仿射变换)下不变的几何性质和不变量。如共线性、平行性和单比等。n维仿射空间的构成如下：设V是一个n维向量空间，A是一个集合，A中的元素称为点，如果对于A中两点P、Q，对应着V中惟一的一个向量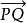，并且这种对应满足：

1.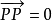(V中的零向量)。

2.任给A中一点P和V中的向量a，在A中存在惟一的点Q，使得。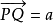

3.对A中三点P，Q，R，有等式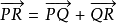，则称A为一个n维仿射空间。特别地，当n=1时称为仿射直线；n=2时称为仿射平面；n=3时称为仿射空间。

在欧几里得平面(空间)中，若不考虑距离的概念，则这个平面(空间)就是一个仿射平面(空间)。如果在仿射平面(空间)中引进无穷远点，则这样的平面(空间)就称为扩大的仿射平面(空间)。在扩大的仿射平面(空间)中，对原有的点与无穷远点不加区别，得到的平面(空间)就是射影平面(空间)。仿射几何中最重要的变换是仿射变换。这种变换的特征是将共线三点变成共线三点。仿射几何中最重要的不变量是单比。其他仿射不变量都可以用单比表示。在仿射平面(空间)中，仿射变换的全体构成一个变换群，称为仿射变换群，简称仿射群。并且在扩大的仿射平面(空间)中，它还是保持无穷远直线(无穷远平面)不变的一个射影变换群。因此，仿射群是射影群的子群，仿射几何是射影几何的子几何。

正交变换一类重要的线性变换。设σ是欧氏空间V的线性变换，如果对V的任意向量α，有(σ(α)，σ(α))=(α，α)，则称σ是V的正交变换。任意欧氏空间V的线性变换σ是正交变换的充分必要条件是：σ保持向量内积不变，即对V中任意向量α，β，有(σ(α)，σ(β))=(α，β)。设V是有限维欧氏空间，σ是V的线性变换，则下列的条件是等价的：2

1.σ是正交变换；

2.σ把V的标准正交基变为标准正交基；

3.σ在标准正交基下的矩阵是正交矩阵。