[科普中国]-铎尔博尔同构

铎尔博尔同构（Dolbeault isomorphism）是由铎尔博尔复形产生的上同调群与由算子a核的等价类所产生的群同构。

简介铎尔博尔同构是由铎尔博尔复形产生的上同调群与由算子a核的等价类所产生的群同构。1

设x是n维复流形，铎尔博尔复形为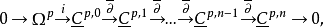层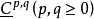是精细层，因而有铎尔博尔同构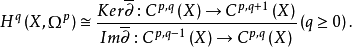

铎尔博尔复形铎尔博尔复形是由复流形的C模序列与算子∂与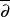构成的复形。

设X是n维复流形，对于p,q≥0，有下述铎尔博尔复形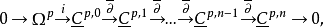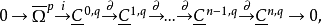其中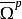表示反全纯丛ΛX'的反全纯截面的芽层。

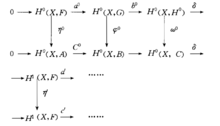
同构两个数学系统（例如两个代数系统），当它们的元素及各自所定义的运算一一对应，并且运算结果也保持一一对应，则称这两个系统同构，记为≌。它们对于所定义的运算，具有相同的结构。例如，十进制数与二进制数是同构的。

建立同构关系的映射，称为同构映射。

本词条内容贡献者为:

杜强 - 高级工程师 - 中国科学院工程热物理研究所