[科普中国]-铎尔博尔复形

铎尔博尔复形（Dolbeault complexes）是由复流形的C模序列与算子构成的复形。

简介铎尔博尔复形是由复流形的C模序列与算子∂与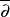构成的复形。

设X是n维复流形，对于p,q≥0，有下述铎尔博尔复形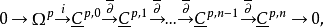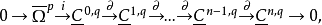其中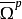表示反全纯丛Λ0,qX'的反全纯截面的芽层。1

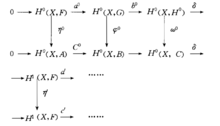
复流形在数学中，特别是在微分几何和代数几何中，复流形是具有复结构的微分流形，即它能被一族坐标邻域所覆盖，其中每个坐标邻域能与n维复线性空间中的一个开集同胚，从而使坐标区域中的点具有复坐标 (z1,…,zn)，而对两个坐标邻域的重叠部分中的点，其对应的两套复坐标之间的坐标变换是全纯的。称n为此复流形的复维数。

一个n维复流形也是2n维的（实）微分流形。

复形复形是组合拓扑的基本概念之一，许多种拓扑空间的研究都可化归为复形拓扑性质的研究，复形是不同维的正常分布的单纯形之总和，即复形中任意两个单纯形，或不相交，或仅具有公共边界等。

此外，复形中单纯形所有边界均属于单纯形，复形中单纯形最高维数称之为复形的维数。

本词条内容贡献者为:

杜强 - 高级工程师 - 中国科学院工程热物理研究所