[科普中国]-梅特罗波利斯－黑斯廷斯算法

梅特罗波利斯－黑斯廷斯算法（英语：Metropolis–Hastings algorithm）是统计学与统计物理中的一种马尔科夫蒙特卡洛（MCMC）方法，用于在难以直接采样时从某一概率分布中抽取随机样本序列。

简介梅特罗波利斯－黑斯廷斯算法（英语：Metropolis–Hastings algorithm）是统计学与统计物理中的一种马尔科夫蒙特卡洛（MCMC）方法，用于在难以直接采样时从某一概率分布中抽取随机样本序列。得到的序列可用于估计该概率分布或计算积分（如期望值）等。梅特罗波利斯－黑斯廷斯或其他MCMC算法一般用于从多变量（尤其是高维）分布中采样。对于单变量分布而言，常会使用自适应判别采样（adaptive rejection sampling）等其他能抽取独立样本的方法，而不会出现MCMC中样本自相关的问题。

该算法的名称源于美国物理学家尼古拉斯·梅特罗波利斯与加拿大统计学家W·K·黑斯廷斯。1

算法假设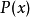为目标概率分布。梅特罗波利斯－黑斯廷斯算法的过程为：

1.初始化：

选定初始状态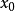；令；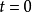

2.迭代过程:

**生成：**从某一容易抽样的分布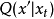中随机生成候选状态；

**计算：**计算是否采纳候选状态的概率；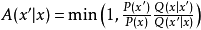

接受或拒绝：

从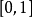的均匀分布中生成随机数；

如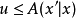，则接受该状态，并令；

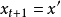如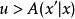，则拒绝该状态，并令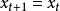（复制原状态）；

**增量：**令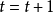.2

马尔科夫蒙特卡洛马尔科夫蒙特卡洛（英语：Markov chain Monte Carlo，MCMC）方法（含随机游走蒙特卡洛方法）是一组用马氏链从随机分布取样的算法，之前步骤的作为底本。步数越多，结果越好。

创建一个具有期望属性的马氏链并非难事，难的是如何决定通过多少步可以达到在许可误差内的稳定分布。一个好的马氏链具有快速混合——从开始阶段迅速获得的一个稳定状态——请参考马氏链最大时间。

因于初始样本，最常见的MCMC取样只能近似得到分布。复杂的MCMC改进算法如过往耦合，但是会消耗更多的计算资源和时间。

典型用法是模拟一个随机行走的行人来进行路径优化等。每一步都算作是一个状态。而统计经过次数最多的地方将在下一步中更有可能为目的地。马氏蒙特卡洛方法是一种结合了蒙特卡罗法的解决方案。但不同于以往的蒙特卡洛integration是统计独立的，MCMC中的是统计相关的。

本方法的相关应用包括：贝叶斯统计、计算物理、计算生物以及计算语言学，此外还有Gill先生的一些著作。3

参见贝叶斯推理

本词条内容贡献者为:

李嘉骞 - 博士 - 同济大学