[科普中国]-相对论性波动方程-

在物理学中，特别是相对论量子力学（RQM）及其在粒子物理学中的应用，相对论波动方程（Relativistic wave equations）预测了粒子在高能量和速度下的行为，与光速相当。在量子场论（QFT）背景下，相对论性波动方程确定了量子场的动力学。

简介相对论波动方程预测了粒子在高能量和速度下的行为，与光速相当，确定了量子场的动力学，常应用在相对论量子力学、粒子物理学等。

方程的解通常表示为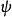（希腊语psi），在相对论量子力学中被称为“波函数”，在量子场论中被称为“场”。由于它们具有波动方程的数学形式或者由拉格朗日密度和场理论的欧拉 - 拉格朗日方程生成，因此方程本身被称为“波动方程”或“场方程”。

在薛定谔图中，波函数或场是薛定谔方程的解：

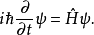上述是量子力学的一个假设。所有相对论性波动方程可以通过指定各种形式的哈密顿算符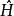构造来描述量子系统。或者，费曼路径积分公式中使用拉格朗日算子而不是哈密顿算子。1

更一般地，相对论波动方程背后的现代形式主义是洛伦兹群理论，其中粒子的自旋与洛伦兹群的表示相对应。

方程以下等式具有满足叠加原理的解，即波函数是加性的。在整个过程中，使用了张量指数表示法和Feynman斜线表示法的标准惯例，包括希腊指数，其中空间分量取值1,2,3，索引量的时间分量取0。波函数被表示为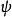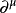，是部件的四梯度算子2。

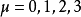在矩阵等式中，泡利矩阵被表示为，其中，其中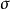是2×2单位矩阵：

其他矩阵有其一般的表示，表达式

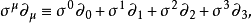是一个2×2矩阵算子，作用于双分量旋量场。

伽玛矩阵表示为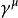，其中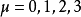，有许多方式方式可以选择，矩阵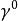是不一定是4×4单位矩阵，表达式：

是一个4×4矩阵算子，作用于4分量的旋量场。