[科普中国]-l∞空间

在数学中，Lp空间是由p次可积函数组成的空间；对应的ℓp空间是由p次可和序列组成的空间。它们有时叫做勒贝格空间，以昂利·勒贝格命名（Dunford & Schwartz 1958，III.3），尽管依据Bourbaki (1987)它们是Riesz (1910)首先介入。在泛函分析和拓扑向量空间中，他们构成了巴拿赫空间一类重要的例子。l∞空间是一种所有有界数列构成的空间。

简介在数学中，Lp空间是由p次可积函数组成的空间；对应的ℓp空间是由p次可和序列组成的空间。它们有时叫做勒贝格空间，以昂利·勒贝格命名（Dunford & Schwartz 1958，III.3），尽管依据Bourbaki (1987)它们是Riesz (1910)首先介入。在泛函分析和拓扑向量空间中，他们构成了巴拿赫空间一类重要的例子。l∞空间是一种所有有界数列构成的空间。1

可数维度空间的p-范数有限维空间中的p-范数可以如{\displaystyle \mathbb {R} ^{n}}一般定义。当空间维数是可数无限时，也可以将p-范数的定义拓展到其上。这个定义一般适用于由数列或序列构成的空间，称为{\displaystyle \ell ^{2}}空间。常见的有如下例子：

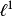空间，所有绝对收敛级数列构成的空间；

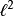空间，所有平方收敛级数列构成的空间；

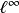空间，所有有界数列构成的空间。

事实上，序列集合上可以自然地按照序列的加法和数乘定义出向量空间。而{\displaystyle \ell ^{p}}空间则是在这个向量空间中定义如下的p-范数：

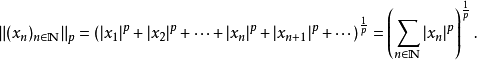然而，上式中右侧的级数不总是收敛的（有可能其级数和是无穷大）。所以l空间实际上是所有序列集合中，令上式右侧的级数能够收敛的元素组成的子集。

可以证明，随着p增大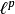， 空间包含的元素也越多。实际上，如果p